What Is XNPV Excel Function?
The XNPV Excel function is used to calculate the net present value of cash flows that are not necessarily periodic. Unlike the traditional NPV function, XNPV takes into account the exact dates of each cash flow, allowing for a more accurate valuation when dealing with irregular payment schedules. It is categorized under financial functions and is particularly useful in financial analysis and investment decision-making, as it provides a more precise measure of an investment’s worth by discounting cash flows based on their specific timing.
For example, Mr. Rohn has invested $100 in an XYZ bond at the discount rate of 2%. Let us calculate the XNPV of the investment.

=XNPV(C2,B3:B4,A2:A4) the result comes as $599.98.

Table of contents
Key Takeaways
- The XNPV Excel function evaluates the net present value of an investment or project with irregular cash flows.
- The NPV function takes cash flows that are evenly spaced over time; XNPV allows users to input specific dates for each cash flow, enabling a more precise calculation.
- Investors can make more informed decisions about whether or not to proceed with a particular project based on its true economic value using the XNPV Excel function.
- This function is used in financial analysis and risk assessment, ultimately leading to more strategic investment decisions with potentially higher returns.
Syntax

- Rate – (Mandatory) The discount rate will be applied throughout the period.
- Values – (Mandatory) This array consists of numeric values that represent both payments and income. Negative values indicate outgoing payments, resulting in negative cash flow. Positive values signify income, leading to positive cash flow.
- Dates – (Mandatory) This is a series of dates that correspond to a series of payments. The date array should be the same length as the values array to ensure accuracy and consistency in the data.
How To Use the XNPV Function in Excel?
In order to effectively utilize the XNPV function in Excel, please follow the steps outlined below.
#1 – Access from the Excel ribbon
Step 1: Choose an empty cell. Then, go to the Formulas tab and click on it.
Step 2: Select the “Financial” option.
Step 3: To continue, go to the drop-down menu and choose XNPV.
Step 4: The Function Arguments window will be displayed. You have to input the values for the “rate,” “values,” and “dates” fields. After completing this step, proceed by clicking on the OK button to continue.

#2 – Enter the worksheet manually
Step 1: To designate an empty cell for the output, simply enter the formula =XNPV() in the desired cell. Alternatively, you can type =X and then promptly double-click on the XNPV function from Excel’s extensive list of suggestions.

Step 2: In order to achieve the desired outcome, kindly press the Enter key.

Examples
Example #1 – Calculate cash flows at the end of a period
Investor X invested in the equity of a company from 2000 to 2003 with a 10% rate of interest. Here, we calculate the net present value of cash flows at the end of a period with an example that will show the XNPV function’s capabilities.
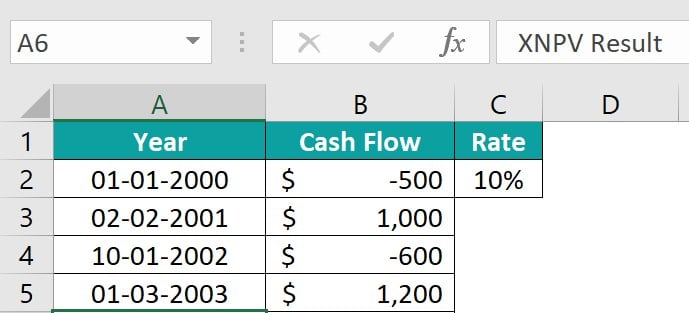
To calculate the outcome, follow the subsequent steps:
Step 1: Select cell B6 and enter the XNPV formula to calculate the accrued interest value.
= XNPV (C2,B2:B5,A2:A5)

Step 2: Enter the references containing the values and press Enter. The result is displayed in cell B6.

Example #2 – Calculate cash flows at the start of a period
In this example, Ms. Diana made a one-time investment in her friend’s company of $1000 at a 12% rate of interest. Now, to calculate the net present value of cash flows at the start of a period, i.e., at the same date every year but before the period’s end, you have to multiply the NPV by (1+rate).

Step 1: Initiate the calculation by entering the XNPV formula in cell B6:
= XNPV (C2, B2:B5, A2:A5)*(1+C2)
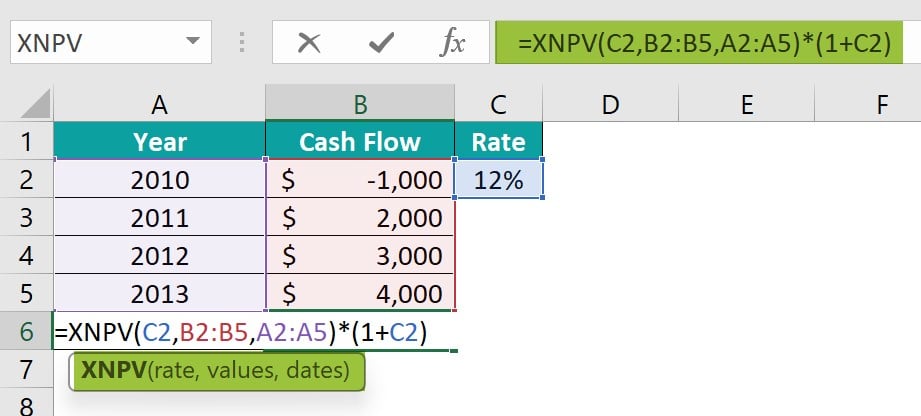
Step 2: The result will be displayed in cell B6, as shown below.

Example #3 – Calculate cash flows at different periods
Mr. Peter invested in a shoe company, making a $0 investment in the first year and then $500 in the second year at a 20 % rate of interest. Now, to calculate the net present value of cash flows at the different periods, you can use the XNPV Excel function.
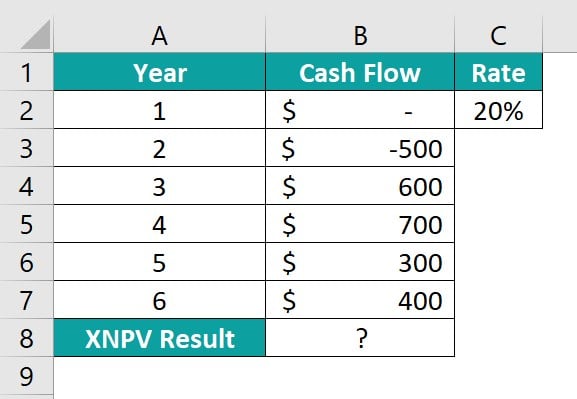
To use the XNPV Excel function, follow these steps:
Step 1: Choose cell B8 and insert the XNPV formula to calculate the accrued interest value as shown below:
= XNPV (C2, B2:B7, A2:A7)

Step 2: Press Enter. It shows that the value is $1,497.01, which is the net present value of the cash flows made in different periods.

XNPV Excel vs. NPV Excel Functions
XNPV Excel and NPV Excel functions both calculate the Net Present Value of an investment, but they differ in their approach and accuracy.
- The key difference lies in cash flows that are not evenly spaced over time. While NPV assumes that cash flows occur at regular intervals, the XNPV allows for irregular cash flow patterns by taking into account specific dates for each cash flow.
- The XNPV requires the user to input the specific date of each cash flow, whereas NPV only requires the initial outlay and subsequent cash flows as inputs.
- The XNPV is considered to be a more sophisticated and flexible function compared to NPV when it comes to evaluating investments with complex or irregular payment schedules.
Important Things To Note
- The #NUM! error occurs when the values and date arrays are of different lengths, or when any of the other dates are earlier than the start date. This error can be caused by discrepancies in the length of arrays or by dates that precede the designated start date.
- The #VALUE! error occurs when either the values or rates arguments are non-numerical or when Excel does not recognize the given dates as valid dates.
- The XNPV analyses investments with varying payment schedules. By discounting each cash flow at its respective date based on a specified discount rate, XNPV provides a more accurate representation of the actual value of an investment.
Frequently Asked Questions (FAQs)
While using the XNPV Excel function, there is no inherent limit to the number of cash flows that can be inputted. The XNPV function allows for an unlimited number of cash flows to be included in the calculation, making it a versatile tool for analyzing a wide range of financial scenarios. The cash flows are added, the complexity and computation time of the function may increase.
While troubleshooting errors using the XNVP function in Excel, check all required arguments are input correctly and that the syntax is correct. The range of cells referenced for the formula contains numerical values only. Check all date values are valid dates and entered in the correct format recognized by Excel.
Let’s look into the example below to understand the errors that can pop up when using the XNPV Excel function. The table we have here presents a bunch of values in a dataset that we can analyze.
To make use of the formula, it’s as easy as typing it in cells B5 & E5, like this:
=XNPV(C2,B2:B4,A2:A4) in cell B5, which causes a #VALUE! error because we entered non-numeric values.
=XNPV(C2,E2:E4,D2:D4) in cell E5, which causes a #NUM! error because one of the dates is missing.
The limitations of using the XNPV function in Excel are as follows;
• The XNPV function assumes all cash flows should be at the exact specified dates, which may differ in reflecting real-world scenarios where payments may be made on different dates.
• The XNPV function does not reinvestment cash flows at an alternative rate, potentially skewing results.
• The XNPV function takes input as a discount rate as a separate parameter, which can generate errors if the wrong rate is used or if rates change over time.
• The XNPV function uses manual inputs of cash flow amounts and dates; there is human error in data entry, which can impact the accuracy of results.
Download Template
This article must help us understand the XNPV Excel Function’s formula and examples. You can download the template here to use it instantly.
Recommended Articles
Guide to XNPV Excel Function in Excel & its meaning. Here we explain how to use the XNPV along with examples & vs NPV. You can learn more from the following articles –

Leave a Reply