NORM.DIST Excel Function

What Is NORM.DIST Function In Excel?

The NORM.DIST function in Excel is an inbuilt Statistical function. It determines the Cumulative Normal Distribution Function or Normal Probability Density Function for the given mean value and standard deviation. Users can use the NORM.DIST Excel functions in statistical and financial activities such as hypothesis testing and stock rate assessment.

For example, the table below contains two input value sets needed to determine the required normal distributions.

And suppose we need to determine and display the two normal distributions specified in cell range A9:A10 in target cell range E9:E10. Then, using the NORM.DIST Excel function in the target cells, we can get the required results.

In the above example, the NORM.DIST Excel function format in cell E9 gives the Cumulative Normal Distribution Function for Value Set 1, as the distribution type is TRUE.

On the other hand, the NORM.DIST Excel function value in cell E10 is the Normal Probability Density Function for Value Set 2, as the distribution type is FALSE.

What Is NORM.DIST Function In Excel?

The Normal Distribution the function returns is, typically, the Cumulative Distribution Function or Probability Density Function.
The function finds application in requirements such as hypothesis testing and risk-return analysis.
The NORM.DIST excel function formula is =NORM.DIST(x,mean,standard_dev,cumulative), where all four mandatory arguments, x, mean, standard_dev, and cumulative, as input. The cumulative argument value must be TRUE when we require the NORM.DIST function to return the Cumulative Distribution Function. And its value should be FALSE when its output has to be the Probability Density Function.

NORM.DIST() Excel Formula

The NORM.DIST Excel function format is:

where,

x: The value we require to determine the distribution for using the NORM.DIST Excel function.
mean: The distribution’s arithmetic mean.
standard_dev: The distribution’s standard deviation.
cumulative: A logical value indicating the function or distribution type. When the argument value is TRUE, the NORM.DIST Excel function returns the Cumulative Normal Distribution Function. And if it is FALSE, the NORM.DIST() output is the Normal Probability Density Function.

All four NORM.DIST Excel function arguments are mandatory.

And considering the following points, ensure to avoid the condition of the NORM.DIST Excel function not working.

If any of the first three NORM.DIST Excel function arguments are not numbers, or the last argument is not a logical value, the NORM.DIST() output will be the #VALUE! error.
Suppose the standard_dev argument value is less than or equal to 0, the NORM.DIST Excel function value will be the #NUM! error.
The NORM.DIST() output will be the Standard Normal Distribution when the mean is 0, the standard deviation is 1, and the cumulative is TRUE.

Excel VBA – All in One Courses Bundle (35+ Hours of Video Tutorials)

If you want to learn Excel and VBA professionally, then Excel VBA All in One Courses Bundle (35+ hours) is the perfect solution. Whether you’re a beginner or an experienced user, this bundle covers it all – from Basic Excel to Advanced Excel, Macros, Power Query, and VBA.

Start Learning Now

How To Use NORM.DIST Excel Function?

The steps to apply the NORM.DIST Excel function are as follows:

Ensure the NORM.DIST() input values have the required data format.
Next, select the required target cell, and enter the NORM.DIST().
Finally, press Enter to get the required normal distribution.

The following example explains the above steps effectively to help us avoid the scenario of the NORM.DIST Excel function not working.

The table below contains the NORM.DIST() argument values to determine the Cumulative Normal Distribution Function.

And suppose the requirement is to display the calculated normal distribution value in cell D9.

Then we can use the NORM.DIST() in the target cell and achieve the required result.

Select the target cell D9, and enter the NORM.DIST() in the following manner.

First, type the function name and an open parenthesis. And then, enter the references to the values in cell range C3:C5 as the first three arguments.

Then, once we enter a comma, Excel will show a drop-down list to enter the cumulative argument. And as we require the Cumulative Normal Distribution Function, double-click the first option, TRUE.

And once we close the parenthesis and press Enter, the function will get executed.

Entering the argument values in the following ways will also give the same result.
=NORM.DIST(C3,C4,C5,C6)

=NORM.DIST(140,110,20,TRUE)

However, the alternative way of applying the NORM.DIST() in the target cell is by selecting the required cell and clicking Formulas → More Functions → Statistical → NORM.DIST. This action will open the Function Arguments window.

Next, enter the required values in the corresponding argument fields in the Function Arguments window.

We can provide the values directly in the fields instead of the cell references to the values.

And once we click OK, the NORM.DIST() gets executed in the target cell D9.
Thus, the NORM.DIST() output gives the cumulative probability. It implies that thechance of a value being 140 or less is 93.3%.

Examples

Check out the following NORM.DIST Excel function examples to understand the topic effectively.

Example #1

The below table shows a list of students in their height order.

And suppose the requirement is to determine the Normal Probability Density Function for the given height values and display the result in column C. Then, applying the NORM.DIST Excel function in the target cells will get us the required data.

But first, we need to determine the given distribution’s mean and standard deviation.

Step 1: To begin with, select cell B13, enter the AVERAGE excel function, and then, press Enter.

=AVERAGE(B2:B11)

Step 2: Next, select cell B14, enter the STDEV.P(), and press Enter.

=STDEV.P(B2:B11)

Step 3: Then, select the target cell C2, enter the NORM.DIST Excel function, and then, press Enter.

=NORM.DIST(B2,$B$13,$B$14,0)

Step 4: Use the fill handle in Excel to apply the formula in the cell range C3:C11.

Mathematically, the following expression represents the NORM.DIST(), when the cumulative argument is FALSE.

where,

x: The independent variable for which we require to apply the function.
µ: The distribution’s mean value.
σ²: The variance.

We shall introduce a new column in the above table to show how the above mathematical expression works.

Step 5: Select cell D2, enter the below formula, and press Enter. It represents the above mathematical expression.

=(1/(SQRT(2*PI())*$B$14))*EXP(-((B2-$B$13)*(B2-$B$13))/(2*$B$14*$B$14))

Step 6: Using the fill handle, apply the formula in the cell range D3:D11.

The above expression uses the SQRT(), PI(), and EXP() to apply the mathematical formula of the NORM.DIST(), with cumulative = 0.

Now, let us see the Normal Probability Density Function output graphically.

Step 7: Select the cell range B1:C11 and go to Insert → Scatter (X, Y) → Scatter with Smooth Lines.

Step 8: Click the chart area to enable the Chart Elements option. And check the Axis Titles option.

Next, update the axes titles by selecting the respective elements in the chart area to get the below chart.

We get a bell curve representing the Normal Probability Density Function. And the graph shows that there is an 18% chance of a student being 62.5 inches tall.

On the other hand, if we need to determine the Cumulative Normal Distribution Function for the given distribution, all the argument values remain the same except cumulative. It will take the value TRUE.

Step 9: Now, let’s modify the table, enter the below formula in cell C2, and press Enter.

=NORM.DIST(B2,$B$13,$B$14,1)

Step 10: Copy the formula in the range C3:C11 using the fill handle.

The above result implies that thechance of a student being 63 inches or less is 59%.

And determining the integral of the previously mentioned mathematical expression from -∞ to x of the specified formula will get the above data.

Further, we can graphically represent the above data following steps 7 and 8, except the chosen cell range will be B1:C11 in the above table.

As the height values are in ascending order, it helps determine the cumulative probability, which the NORM.DIST() returns, as shown above. Also, it is the reason for achieving the above graphs.

Example #2

Consider that person X states that his age is above 35. And assume the population’s mean age is 30 and the standard deviation for age is 5.

And suppose the requirement is to determine and display the probabilities of person X’s age being above and precisely 35 in cells E9:E10. Then, applying the NORM.DIST Excel functionin the target cells will get us the required result.

To calculate the probability of person X’s age being above 35, we need to determine the Cumulative Normal Distribution Function.

Step 1: Select the target cell E9, enter the below NORM.DIST Excel function, and press Enter.

=NORM.DIST(C3,C4,C5,C6)

The result shows a 16% chance of person X being 35 or above of age.

However, the Normal Probability Density Function will give us the probability of person X’s age being precisely 35.

Step 2: Select the target cell E10, enter the below formula, and press Enter.

=NORM.DIST(D3,D4,D5,D6)

The output shows that close to 4.8% of the population is aged 35.

Example #3

Consider the below table containing the stock rate data of a company.

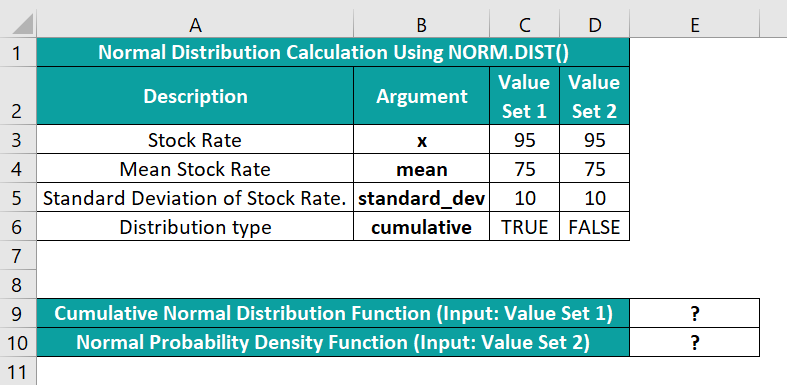
And suppose the requirement is to calculate the probability of the stock rate to be 95 or less and display the outcome in cells E9:E10.

Then, applying the NORM.DIST Excel functionin the target cells in the following ways will fetch us the required result.

Step 1: Select the target cell E9, enter the NORM.DIST(), and press Enter.

=NORM.DIST(C3,C4,C5,C6)

The NORM.DIST Excel functionoutput shows that close to 98% of the stocks have a rate of 95 or less.

Step 2: Select the target cell E10, enter the NORM.DIST(), and press Enter.

=NORM.DIST(D3,D4,D5,D6)

The NORM.DIST() output shows that 0.53% of the stocks have a rate of 95.

Important Things To Note

The NORM.DIST Excel function calculates the Normal Distributions for the specified mean value and standard deviation
Suppose the first three arguments are non-numeric, or the last argument is not a logical value, then, the NORM.DIST Excel function returns the #VALUE! error.
For a standard_dev argument value less than or equal to 0, the NORM.DIST functionoutputis the #NUM! error.
For a mean value of 0, a standard deviation of 1, and a cumulative value of TRUE, the NORM.DIST function returns the standard normal distribution.
All four NORM.DIST Excel function arguments are mandatory.

Frequently Asked Questions (FAQs)

1. How can you apply the NORM.DIST function in Excel VBA?

You can apply the NORM.DIST function in Excel VBA using the method:

Application.WorksheetFunction.Norm_Dist(Arg1,Arg2,Arg3,Arg4)

The specified arguments in the above method interpret as the NORM.DIST function arguments, as explained in the NORM.DIST() Excel Formula section.
The below example explains how to apply the above method.

The following table contains the input data required to compute the Cumulative Normal Distribution Function for a given population.

And suppose the requirement is to display the result in cell D9. Then, here is how we can use the method mentioned above to apply the NORM.DIST() in Excel VBA and achieve the required output in the target cell.

• Step 1: First, open the worksheet containing the above table open, and then, press the keys Alt + F11 to access the VBA Editor.

• Step 2: Next, pick the required VBAProject and select the Module option in the Insert tab to access a new module window, Module1.

• Step 3: Then, enter the VBA code in the Module1 window to apply the NORM.DIST().

Sub NORM_DIST_fn()

Range(“D9”) = Application.WorksheetFunction.Norm_Dist(Range(“C3”), Range(“C4”), Range(“C5”), Range(“C6”))

End Sub

• Step 4: Execute the code by clicking the Run Sub/UserForm button.

• Step 5: Open the active worksheet to view the result in the target cell D9.

The result shows that the probability of a value in the given population being 200 or less is about 82%.

2. What is the difference between the NORM.DIST() and NORM.S.DIST()?

The difference between the NORM.DIST() and NORM.S.DIST() is that the NORM.DIST() determines the Normal Distribution for the given mean value and standard deviation. And the function can calculate the Cumulative Distribution Function or Probability Density Function.
On the other hand, the NORM.S.DIST() computes the Standard Normal Distribution for a mean value and standard deviation of 0 and 1, respectively.

3. Why is the NORM.DIST Excel function not working?

The NORM.DIST Excel function is not working, perhaps because of the following reasons:
• The first three arguments supplied are not numbers.
• The last argument provided is not a logical value.
• The supplied standard_dev is less than or equal to 0.

Download Template

This article must be helpful to understand the NORM.DIST Excel Function, with its formula and examples. You can download the template here to use it instantly.

NORM.DIST Excel Function Download

NORM.DIST Excel Function