What Is BINOM.INV Excel Function?
The BINOM.INV Excel function is categorized under statistical function, which calculates the inverse of the binomial cumulative distribution. The function allows users to determine the least value for which the cumulative binomial distribution is larger than or equal to a given probability.
The BINOM.INV Excel function is helpful in fields such as economics, finance, and biology. To use BINOM.INV effectively, we must input three values:
- The number of trials
- The desired number of successes
- The probability of success for each trial
We will explore the application of the BINOM.INV Excel function in the below example. The data in the table is neatly organized as follows:
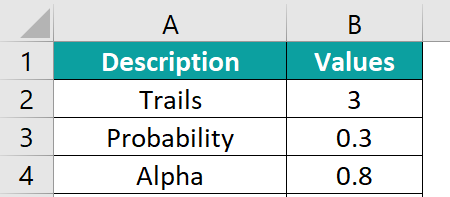
To obtain the desired output in cell B5, enter the formula precisely as shown below: = BINOM.INV(B2, B3, B4). Press the Enter key. The calculated value appears in cell B5, just as depicted in the provided image. The BINOM.INV function can be used to find occurrences such as the probability of getting a head when you toss a coin ten times or the number of defective items in a batch during production.

Table of contents
Key Takeaways
- The BINOM.INV function in Excel allows professionals to determine the smallest value for the cumulative binomial distribution is less than or equal to a given probability.
- With the number of trials, probability of success, and desired probability, we can estimate the critical value required to attain a result in a binomial experiment.
- The professionals analyze datasets with binary results by statistical evidence. With its syntax and capabilities, BINOM.INV professionals calculate complex probabilistic problems easily.
Syntax

The BINOM.INV function includes the following arguments:
- Trials – (Required) It shows the number of Bernoulli trials, which depends on the total number of independent trials to be performed. If a decimal value is entered, Excel will automatically turn it into an integer.
- Probability_s – (Required) It shows the probability of achieving success in a single trial.
- Alpha – (Required) It shows the probability of the Cumulative Binomial distribution. This value should be within the range of 0 to 1.
How To Use BINOM.INV Function In Excel?
To effectively utilize the BINOM.INV function in Excel, follow these steps.
#1 – Access from the Excel Ribbon
- Choose the empty cell which will contain the result. Go to the “Formulas” tab and click it.

- Select the “More Functions” option from the menu.

- Select the “Statistical” option from the drop-down list. Select “BINOM.INV” from the drop-down menu.

- A window called “Function Arguments” appears. As the number of arguments, enter the value in the “trials,” “probability_s,” and “alpha.” Select OK.

#2 – Enter the worksheet manually
- Step 1: Select an empty cell for the output. Type “=BINOM.INV()” in the selected cell. Alternatively, type “=B” and double-click the BINOM.INV function from the list of suggestions shown by Excel.

- Step 2: Press the “Enter” key to get the result.
Examples
Example #1
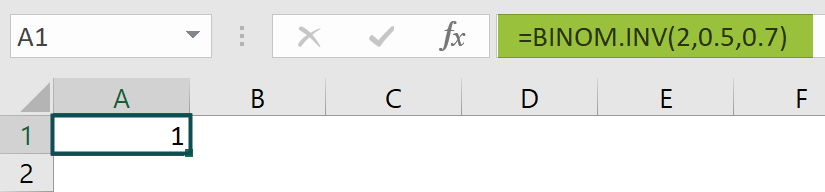
In the following example, we will apply the concept of the BINOM.INV Excel function to find the smallest number of victorious sales in 10 attempts with a probability of success at 0.5, with a cumulative probability of 0.8.
The data within the provided table is organized as follows:
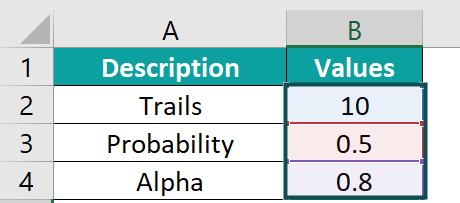
- Step 1: Let us enter the formula in cell B5. We know the formula for BINOM.INV and its arguments. Now, enter the formula exactly as shown below:
= BINOM.INV(B2,B3, B4).
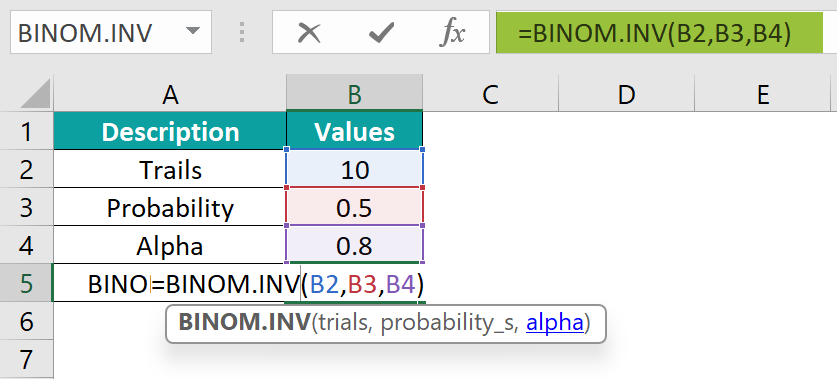
- Step 2: Press the Enter key. The result value is displayed in cell B5, just like in the provided image.

By following these steps, you can easily utilize the BINOM.INV Excel function to calculate probabilities.
Example #2
In this example, we’re going to determine the smallest number of products with a defect in a batch of 200 using the BINOM.INV Excel function that would give a cumulative probability not greater than 0.04 and a defect rate of 0.02. The data in the table is organized like this:
To calculate the desired output in cell B5, here’s what you need to do:
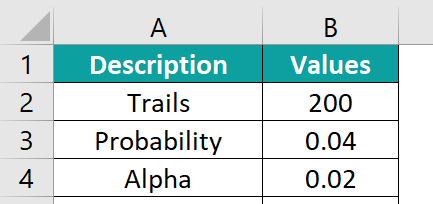
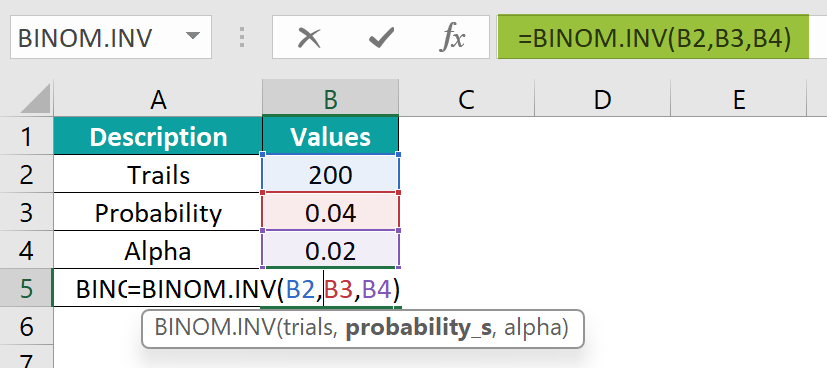
- Step 1: Pick the cell where you want to enter the formula and get the result. Let’s go with cell B5 for this example. Now, enter the formula exactly as shown below:
= BINOM.INV(B2, B3, B4).
- Step 2: Click the Enter key. You’ll see the corresponding value in cell B5, just like in the image provided.
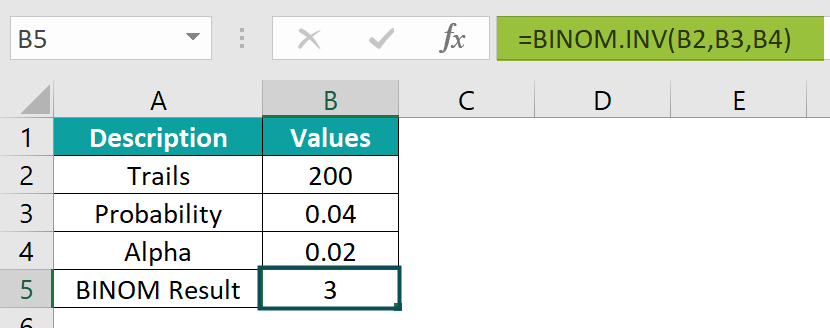
By following these simple steps, you can easily make use of the BINOM.INV Excel function to calculate probabilities.
Example #3
In this example, we will use the concept of the BINOM.INV Excel function and its ability to assist us in calculating probabilities to check the height of the commodity to achieve a success rate of attaining results.
The data in the table is organized as follows:
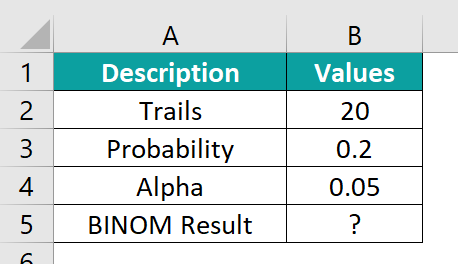
To calculate the desired output in cell B5, here’s what you need to do.
- Step 1: Select the cell where you want to enter the formula and obtain the result. Let’s choose cell B5 for this example. Now, enter the formula exactly as shown below:
= BINOM.INV(B2, B3, B4).
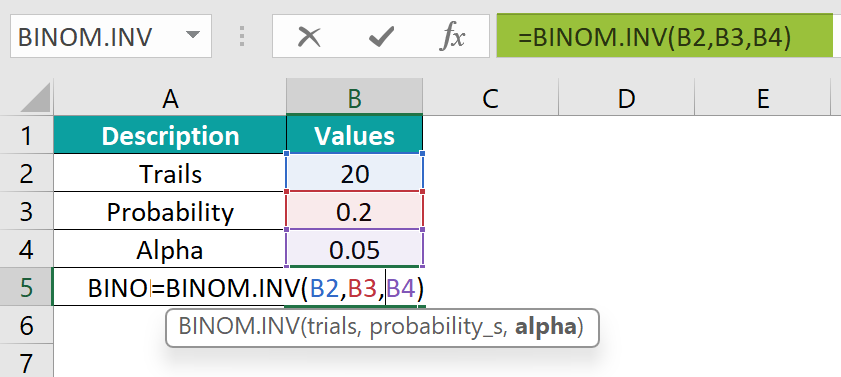
- Step 2: Press the Enter key. You will witness the value appear in cell B5, just like in the provided image.
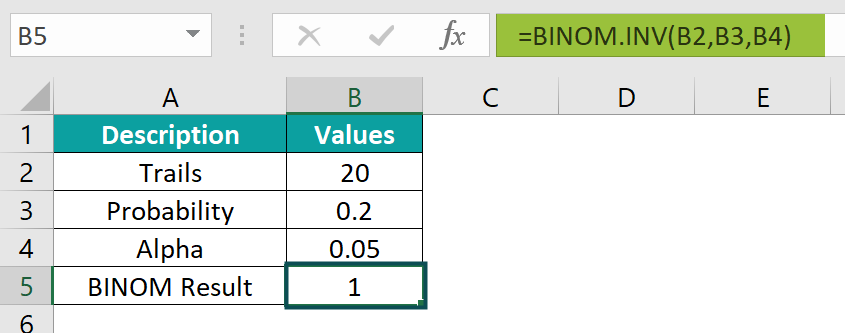
Using the above steps, you can utilize the BINOM.INV Excel function to calculate probabilities.
Important Things to Note
- The #VALUE! error occurs when any of the entered arguments are non-numeric.
- The #NUM! error occurs for three reasons. It is when the trial value is less than zero, when the probability’s value is less than zero or greater than 1 and when the alpha value is less than zero or greater than 1.
Frequently Asked Questions (FAQs)
The purpose of the BINOM.INV Excel Function is to calculate the minimum number of trials required for an entered probability in a binomial distribution. The function is used in statistical analysis and decision-making processes that involve binary outcomes.
In this example, we will explore the concept of the BINOM.INV Excel function and examine how #NUM! The error can occur in a given scenario.
Select the cell B5 to enter the formula. Now, enter the formula exactly as shown below:
=BINOM.INV(B2, B3, B4)
The result is shown in cell B5, just like in the provided image.
The BINOM.INT and BINOM.DIST functions in Excel are both statistical functions in Excel. They are used for calculating binomial distributions.
• The BINOM.INT function calculates the probability of achieving a certain number of successes within a number of trials, with or without entering the cumulative distribution or probability interval, whereas the BINOM.DIST function calculates the estimated probability of attaining a particular number of successes within a fixed range of trials based on probability and trial count.
• The BINOM.DIST function provides an estimated probability value, making it more efficient for larger data sets but sacrificing some accuracy compared to the exact calculations performed by BINOM.INT function.
In this example, we will solve the distinction between the BINOM.INV Excel function and the BINOM.DIST Excel function within a given scenario.
To calculate the desired output in cells B6 and B7, follow these steps and refer to the formula shown in cells C6 and C7: Select cells B6 and B7 to enter the formula. Now, enter the formula exactly as shown below:
=BINOM.INV(B2, B3, B4) and =BINOM.DIST(B2,B3,B4,FALSE)
Once the formula is entered, the result is shown in cell B5, just like in the provided image.
The following are the limitations of using the BINOM.INV function in Excel.
• The function requires the number of trials to be a positive integer and the probability of success to be between 0 and 1 inclusively. The function assumes that each trial is independent and there are only two possible outcomes: success or failure.
• The BINOM.INV function returns a value representing the number of successful trials; it may not provide precise results when dealing with large values of n or p close to 0 or 1.
Download Template
This article must help us understand the BINOM.INV Excel Function’s formula and examples. You can download the template here to use it instantly.
Recommended Articles
Guide to BINOM.INV Excel Function in Excel & its meaning. Here we explain how to use the BINOM.INV Excel for cell references, examples & downloadable excel template. You can learn more from the following articles –





Leave a Reply