What Is Matrix Multiplication In Excel?
Excel Matrix Multiplication is a binary multiplication of two matrices, where the total columns in the first matrix and the total rows in the second matrix are equal. And the output is also a matrix, with the total rows equal to that in the first array and total columns equal to that in the second array.
Excel offers an inbuilt function MMULT to perform Matrix Multiplication in Excel. And users can use the function in fields involving Matrix Multiplication, such as network theory and population modeling.
For example, the following image shows two 2×2 arrays, Array 1 and Array 2. We will find the product of the two matrices using the Matrix Multiplication formula.

Select cell range E7:F8, enter the formula =MMULT(C3:D4,G3:H4), and press “Ctrl + Shift + Enter” to execute as an array formula.
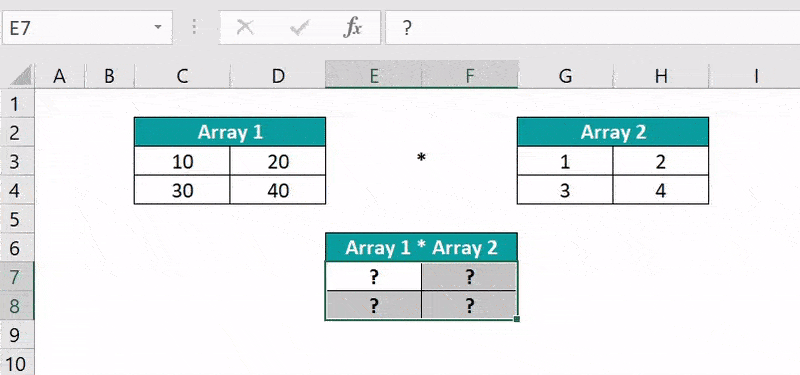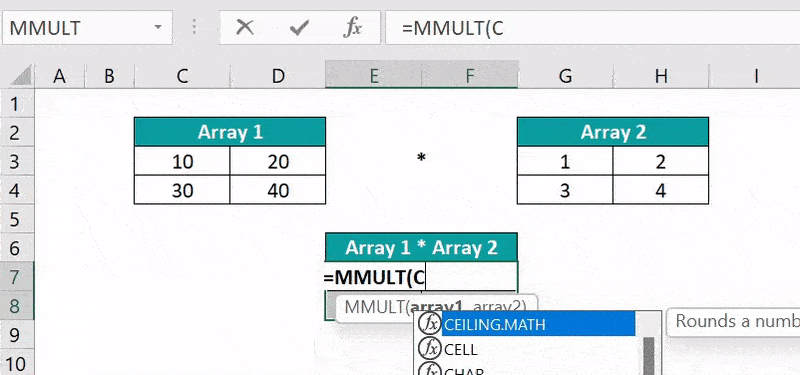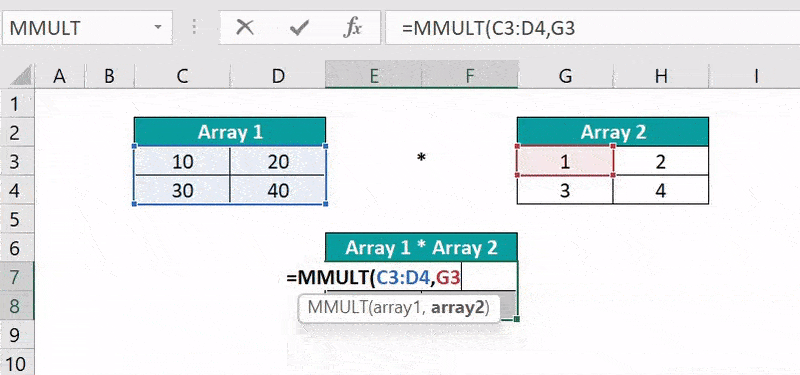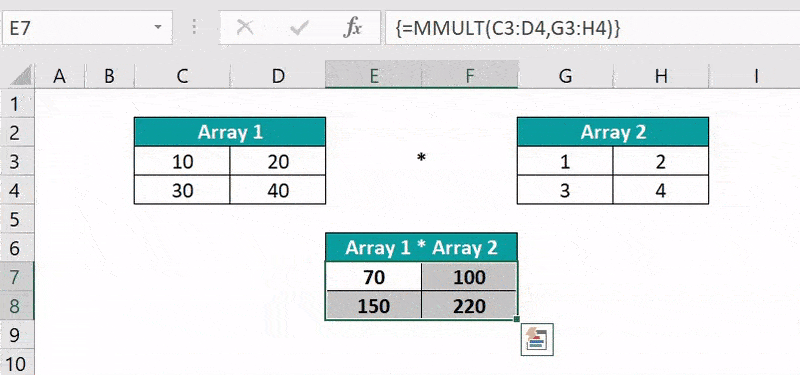
The output is shown above.
We will understand the Matrix Multiplication calculation in cell E7 as follows:
=C3*G3+D3*G4
=10*1+20*3
=10+60
=70
Thus, in this way, the function updates the final product values in the target cell range.
Table of contents
Key Takeaways
- Excel Matrix Multiplication is a method to multiply two arrays of numbers. The product is also a matrix, with the row count equal to the total rows in the first matrix and the column count equal to the total columns in the second matrix.
- We can find the square of a matrix only if the matrix has an equal number of rows and columns.
- Users can use the MMULT function in linear algebra calculations such as linear maps, geometric rotations, and resource allocation in Economics.
Explanation Of The Excel Matrix Multiplication
The Matrix Multiplication, MMULT, accepts the cell ranges of the two given arrays as the input. And then, we execute it as an array formula. So, the function multiplies the corresponding terms from the two matrices and adds the products in each cell of the target matrix, i.e., in one go, returns the product matrix.
The mathematical expression for Matrix Multiplication is:
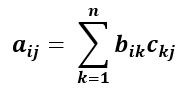
where,
- a: The resulting product array.
- b and c: The two input arrays.
- i: The row number.
- j: The column number.
- n: Counter
Syntax Of Excel Matrix Multiplication Formula
The syntax of the Matrix Multiplication formula is:

The mandatory arguments of the Matrix Multiplication formula are:
- array1 and array2: The two arrays we require to multiply.
How To Do Matrix Multiplication In Excel?
We can do the Excel Matrix Multiplication in 2 ways, namely,
- Access from the Excel ribbon.
- Enter in the worksheet manually.
Method #1 – Access from the Excel ribbon
Choose a target cell range for output → select the Formulas tab → go to the Function Library group → click the Math & Trig option drop-down → select the MMULT function, as shown below.

The Function Arguments window appears. Enter the arguments in the Array1 and the Array2 fields → press Ctrl + Shift + Enter to execute the function as an array formula.

Method #2 – Enter in the worksheet manually
- First, check if the total columns in the first matrix and the total rows in the second matrix are equal.
- Next, select a target cell range for the output. The total rows must be the same as in the first matrix, and the total columns the same as in the second matrix.
- Type =MMULT( in the cell. [Alternatively, type =M or =MM and double-click the MMULT excel function from the Excel suggestions.]
- Enter the arguments as array values or references to array ranges and close the brackets.
- Press Ctrl + Shift + Enter to execute the function as an excel array formula and get the required matrix.
Here is an Excel Matrix Multiplication example to explain the abovementioned steps in detail.
The image below shows two matrices, Array A and Array B, each containing positive and negative numbers. We must multiply the two arrays and display the output as an array.
The number of columns in Array A and the row count in Array B are equal. Thus, we can multiply the two matrices. And the target array dimension will be 2×2, as the total rows in Array A and column count of Array B is 2.

The steps to use the MMULT() formula are,
- Select cell range F7:G8.

- Start entering the MMULT() with the ‘=’ sign, the MMULT function name, the opening bracket, the first array range, and a comma as =MMULT(D3:E4,

- Enter the second array range, and close the brackets. The complete formula is =MMULT(D3:E4,H3:I4).

- Press Ctrl + Shift + Enter to execute the MMULT() as an array formula. {=MMULT(D3:E4,H3:I4)}. The output is shown below.

[Alternatively, select cell range F7:G8, and follow the path Formulas → Math & Trig → MMULT.
The Function Arguments window opens.
Next, enter the given array ranges in the respective fields in the Function Arguments window.
Finally, press Ctrl + Shift + Enter to execute the MMULT() as an array formula in the target cells F7:G8.]
Let us consider cell G8 to check how the formula works.
=D4*I3+E4*I4
=15*(-8)+(-20)*16
=-120-320
=-440
Examples
We will consider some advanced scenarios using the Excel Matrix Multiplication examples.
Example #1 – Multiplying a Matrix with a Scalar Number
We will perform Matrix Multiplication involving a scalar number.
The following image shows a matrix and a scalar number. We will multiply the given matrix by the specified scalar quantity and display the output in the cell range I3:K6.
The reason to choose a 4×3 matrix (cell range I3:K6) for the target array is that the source matrix dimension is 4×3. And multiplying the source matrix by a scalar number will result in a matrix of the same size as the given matrix.

The steps to multiply the matrix are as follows:
- Step 1: Select cell range I3:K6.

- Step 2: Enter the formula =(C3:E6)*G3 to multiply the matrix with the scalar number.

- Step 3: Press Ctrl + Shift + Enter to execute the expression as an array formula and obtain the resulting product array formula, as {=(C3:E6)*G3}

The array formula multiplies each Matrix A element with the scalar number -10 to return the corresponding product value in each cell of the target matrix.
The below image shows the calculations in the target matrix cells, i.e., the output.

Example #2 – Matrix Multiplication of Two Individual Arrays
We will calculate the Excel Matrix Multiplication of different dimensions.
The image below shows two arrays, Array A and Array B. We must find the product of the two individual arrays

The steps to perform Matrix Multiplication using the MMULT() in the target array range are,
- Step 1: The total number of columns in Array A is 4, and the total number of rows in Array B is 4. And as the two values are equal, we can multiply the two arrays.
Furthermore, we have to perform Excel Matrix Multiplication different dimensions. So, we need to be careful while deciding the target array dimensions. In this case, the target matrix size is 3×3, as the total rows in the first array and column count of the second array are 3.
Therefore, select cell range G10:I12.
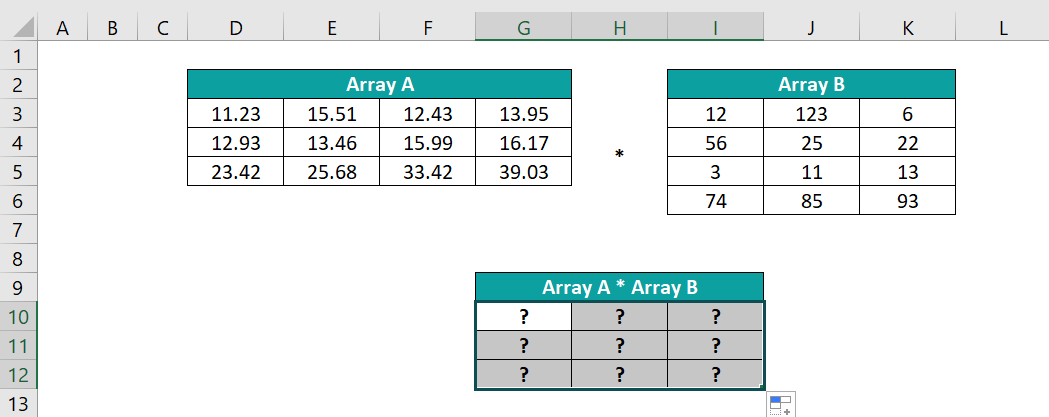
- Step 2: Enter the MMULT() formula =MMULT(D3:G5,I3:K6)

- Step 3: Press Ctrl +Shift +Enter to apply the function as an array formula {=MMULT(D3:G5,I3:K6)}, as shownin the target cell range.

The MMULT() accepts the two individual array ranges. It multiplies the respective terms from the two arrays and adds the products to update the results in the corresponding target array cells.
The Array A * Array B (Formulas In Cells G10:I12) table shows the product array cells’ formulas, which the MMULT() performs in one go. The function work according to the Matrix Multiplication mathematical equation explained in the Explanation section. The output is shown below.

Example #3 – Matrix Multiplication between Arrays with Single Column and a Single Row
We shall see an example shown below of two sets of data, and perform Excel Matrix Multiplication, where the two input arrays contain a single column and row.
- The first set shows two arrays, with the first matrix containing a single column of numbers and the second matrix containing a single row of values.
- On the other hand, the second set includes two arrays, with the first matrix containing a single row of numbers and the second matrix containing a single column of values.

The steps to perform Matrix Multiplication in the two scenarios are as follows:
- Step 1: The total columns in Array 1 and row count in Array 2 are equal, which is 1 in this case. So, we can multiply the two matrices.
Further, as the number of rows in Array 1 is 4 and the number of columns in Array 2 is 3, the product matrix size will be 4×3.
Therefore, select cells B11:D14 as the target 4×3 matrix range.

- Step 2: Enter the MMULT() formula =MMULT(B4:B7,D4:F4)

- Step 3: Press Ctrl + Shift + Enter to execute the function as an array formula and achieve the following product array as {=MMULT(B4:B7,D4:F4)}

- Step 4: The total columns in Array A and row count in Array B are equal, which is 3 in this case. So, we can multiply the two matrices.
Further, as the number of rows in Array A and the column count of Array B is 1, the product matrix size will be one cell.
So, select cell I11 as the target cell, and enter the MMULT() formula =MMULT(I3:K3,J6:J8)
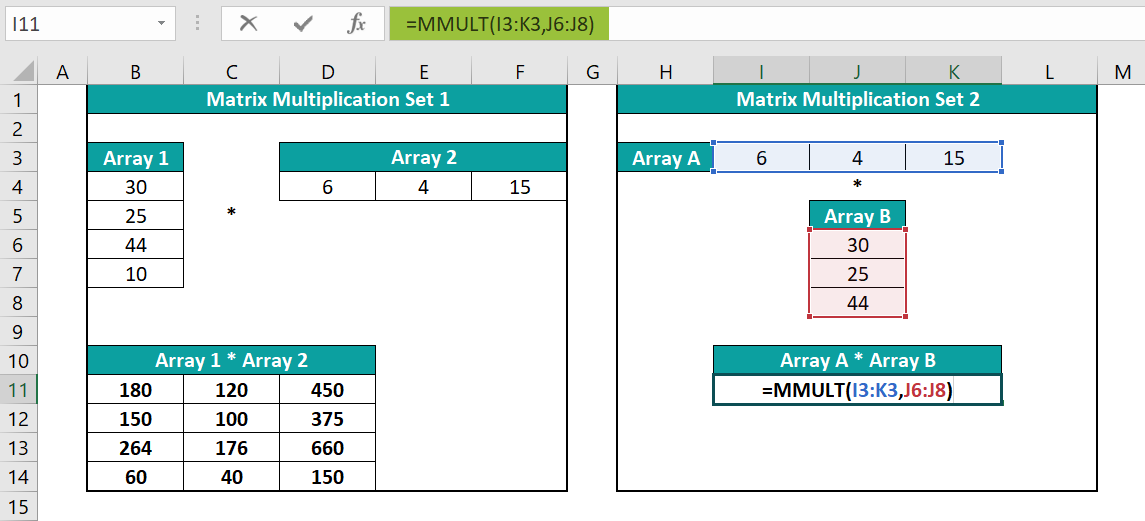
- Step 5: As we require the output in one cell, press Enter to execute the MMULT(), and get the product of the two specified matrices. The output is shown below.

Example #4 – Determining the Square of a Matrix using MMULT in Excel
We can determine the square of a matrix only when it has a square dimension.
[Note: If the number of rows and columns in the given matrix differs, it will be a scenario of multiplying two matrices of different dimensions. And the column count of the first matrix will not equal the number of rows in the second matrix. Thus, as the condition to perform Matrix Multiplication does not hold, we cannot find the square of the given matrix.]
The image below shows a square matrix, Matrix X.

The steps to find the square of the Matrix X using the MMULT() are as follows:
- Step 1: Finding the square of a matrix is equal to multiplying the matrix with itself.
Therefore, the two matrices the MMULT() multiplies will have the same dimensions, 4×4. Thus, as the total rows in the first matrix and column count of the second matrix are 4, the product array will be a 4×4 matrix.
Let us select the cells C8:F11 as the target 4×4 matrix range.

- Step 2: Enter the MMULT() formula =MMULT(C2:F5,C2:F5)

- Step 3: Press Ctrl +Shift +Enter to execute as an array formula as {=MMULT(C2:F5,C2:F5)}.
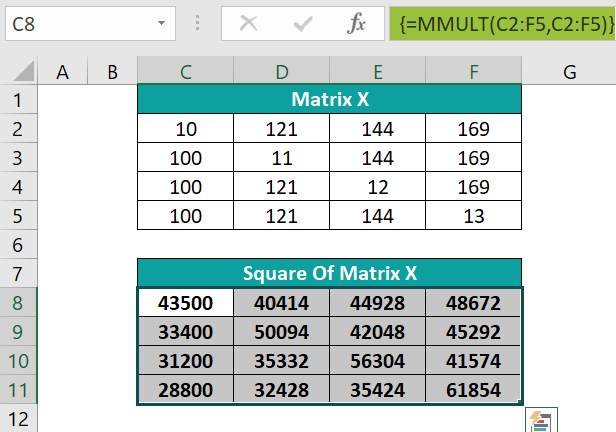
The output is shown above.
Important Things To Note
- Ensure the total columns in the first array and the total rows in the second array are the same to make Excel Matrix Multiplication possible.
- The mandatory two input arrays in the MMULT() can be array constants or numeric cell references.
- Suppose the given matrices contain non-numeric values or blank cells, or the total columns in the first matrix and total rows in the second matrix are unequal. Then, multiplying such matrices will result in the #VALUE! error.
Frequently Asked Questions (FAQs)
We can multiply a 3×3 matrix by a 3×1 using the MMULT function.
Let us see the steps with an example.
The image below shows two matrices. While the first matrix is 3×3, the second is 3×1.
The steps to multiply the two matrices using the MMULT function are as follows:
• Step 1: Select cell range C8:C10.
• Step 2: Enter the MMULT() formula =MMULT(C3:E5,G3:G5)
• Step 3: Press Ctrl + Shift + Enter to execute the MMULT function as an array formula as {=MMULT(C3:E5,G3:G5)}
The MMULT function accepts the 3×3 and 3×1 matrices as input. And as the total columns in the first array and the total rows in the second array are the same, it multiplies the two matrices.
The output is a product matrix, Matrix C, of the dimension 3×1. The total rows are 3, equal to the row count of the first array, and one column, equal to the column count of the second array.
The difference between SUMPRODUCT() and MMULT() is that SUMPRODUCT calculates the sum of products of the corresponding number ranges of the same size.
On the other hand, the MMULT function determines the matrix product of two arrays of the same or different dimensions. However, the condition is that the first matrix’s column count should equal the second matrix’s total row count.
MMULT formula may not work due to the following reasons:
• The number of columns in array1 and the number of rows in array2 are not the same.
• The input matrices contain non-numeric values or empty cells.
Download Template
This article must help understand the Excel Matrix Multiplication, with its formula and examples. We can download the template here to use it instantly.
Recommended Articles
This has been a guide to Excel Matrix Multiplication. Here we explain how to multiply 2 array of numbers or matrices with examples. You can learn more from the following articles –







Leave a Reply